プレスリリース配信元：公益財団法人スプリックス教育財団

スプリックス教育財団 基礎学力と学習の意識に関する保護者・子ども国際調査2025

　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　2025年11月12日

　概要

公益財団法人 スプリックス教育財団（本部：東京都渋谷区／代表理事：常石 博之）は、基礎学力に対する意識の現状を把握することを目的に、「基礎学力と学習の意識に関する保護者・子ども国際調査2025」を実施しました。第4回目の今回は、CBT形式の計算テスト（TOFAS）のデータ分析の結果についてご報告します。

今回の報告での分析対象者は、日本のある公立中学校に通う中学2年生約100名です。解答時間40分・問題数60問（うち最初の20問が中学1年生に学習する内容、残り40問は今年度1学期に習った内容）の計算テスト（TOFAS）のデータを分析した結果、以下の3点が明らかになりました。
調査結果のポイント

(1) 前学年の復習範囲の解答速度とテスト全体の正答率に強い相関
テスト開始直後5分間の正答数（主に前学年の復習範囲の正答数）と、テスト全体の正答率の間には極めて強い正の相関が見られました。前学年の復習範囲を速く正確に処理できる能力が、テスト全体の高い正答率の基礎となることがわかりました。

(2) 高い計算力が自信を生む？
計算の自信とテストの正答率にも相関がありました。しかし、解答速度などと比べると、その影響は限定的でした。そのため、テストの正答率や解答速度などの客観的な計算力の高さが、生徒の主観的な「計算への自信」へとつながっている可能性があります。

(3) 成績層ごとに全く異なるテスト解答戦略
成績上位のグループは序盤で解答が速く、終盤は慎重になる「ペース配分戦略」を取りました。一方、成績が下位のグループほど終盤に解答速度が不自然に急上昇する「駆け込み解答」がみられるなど対照的な解答パターンを示しました。

　調査の背景

GIGAスクール構想の推進に伴い、日本の教育現場ではデジタル化が急速に進んでいます。例えば、従来の紙媒体に代わり、タブレットを用いたデジタル教科書やCBT（Computer-Based Testing）の導入が拡大しています。特に、CBTは個々の解答状況を時系列で記録できるため、これまで把握が難しかった解答速度や時間配分といった、テストの解答戦略を詳細に分析することが可能です。これにより、単なるテストの点数だけでなく、生徒が「どのようにつまずき、どのように問題を解き進めているか」という学習プロセスそのものに焦点を当てることができます。

そこで本レポートでは、CBT形式の計算テスト「TOFAS」の解答ログデータと、意識調査で得られた「計算への自信」に関するデータを活用しました。分析の精度を高めるため、特定の教育環境や生徒層といった条件を揃えられる単一の中学校のデータに注目し、以下の3つの問いについて検証しました。
- 序盤の前学年の復習範囲に対する計算処理速度は、テスト全体の正答率と相関があるのか？
- 客観的指標である「解答速度」と、主観的な「自信」では、どちらがテストの正答率とより強い相関をもつか
- 成績層によって、テスト中の解答戦略にどのような違いが見られるか？

　調査方法

留意事項
・　匿名性保持のため、正確な調査対象者数を非公表としています。
・　本リリースに関する内容をご掲載の際は、必ず「スプリックス教育財団調べ」と明記してください。

　調査結果

(1) 前学年の復習範囲の解答速度とテスト全体の正答率に強い相関
はじめに、テスト開始直後の解答速度とテストの正答率の関係について調べました。


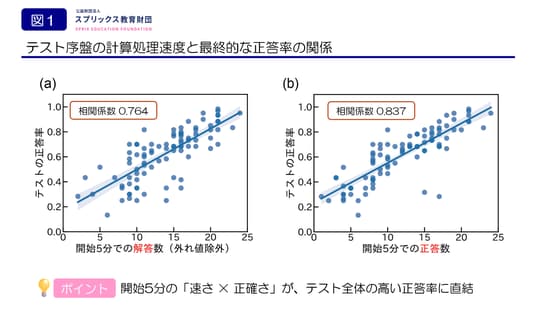
図1. テスト序盤の計算処理速度とテスト全体の正答率の関係　左図(a)は開始5分間での解答数とテスト全体の正答率の関係（相関係数 R=0.764）、右図(b)は開始5分間での正答数とテスト全体の正答率の関係（相関係数 R=0.837）を示しています。

図1(a)は、テスト開始直後5分間での解答数（横軸）とテスト全体の正答率（縦軸）の関係を示しています。ここから、成績上位の生徒ほど序盤の解答速度が速いという正の相関（相関係数：R=0.764）(注1)が見て取れます。しかし、開始５分での解答数の多さにも関わらず極端に正答率が低いデータもありました（注2）。
注1 本報告書で示す相関係数はピアソンの相関係数を指します。一般に、1に近いほど「強い正の相関」が、-1に近いほど「強い負の相関」があることを示します。0に近い場合は、相関がほとんどないと解釈されます。
注2 開始5分間で25問以上解答しながらも、テストの正答率が4割以下だったデータが2件ありました。計算することなく解答を進めた可能性が高いと判断し、図1(a)では外れ値として分析対象から除外しました。

そこで、速さに加えて正確さも考慮したテスト開始直後5分間での正答数（以降、序盤の正答速度と記載）（横軸）とテスト全体の正答率（縦軸）の関係を示したのが図1(b)です。図1(b)では相関係数がR=0.837と非常に高く、テスト開始直後に速いだけでなく、「速さ」と「正確さ」を両立させている生徒ほど、テスト全体の正答率も高くなるという、より強固な関係性が確認できました(注3)。テストの1問目から20問目は、中学１年生の履修範囲で、受験者にとっては前学年の復習範囲です。そのような前学年の復習範囲を速く正確に解く能力が、テスト全体の高い正答率の重要な土台であることを示しています。
注3 開始5分間での解答数や正答数と正答率が線形の関係とは限りません。しかし、ここでは簡単のため線形と仮定して相関係数を計算しています。
（２） 高い計算力が自信を生む？
算数・数学のテストや計算テストにおいて、主観的な「自信」がテストの点数と相関があることは知られています(第一回報告書参照)。では、この主観的な「自信」と、(1)で議論した客観的なテスト序盤の「解答速度」や「正答速度」では、どちらがテストの正答率とより強く相関しているでしょうか。これを比較検討するため、計算への自信（横軸）と、テスト全体の正答率および単元別の正答率（縦軸）の関係を調べました［図2］。

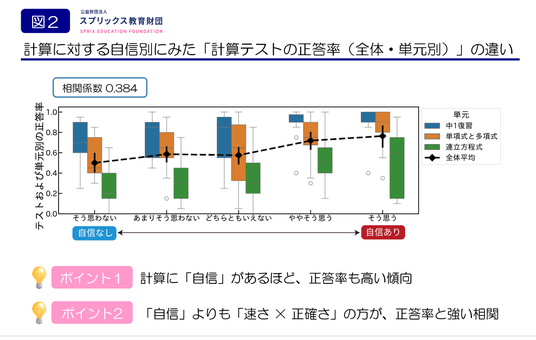
図2. 計算への自信度と、全体および単元別の正答率の関係　「あなたは計算に自信がありますか」という質問への回答別に、テストの正答率を示しています。黒いひし形の点はテスト全体の平均正答率（エラーバーは95%信頼区間）、箱ひげ図は単元ごとの正答率の分布を表しています。

グラフのテスト全体の平均正答率（黒い点）を見ると、「自信がある方が、成績が良い」という正の相関が見られます。しかし、全体の相関係数は0.384と中程度の強さであり、(1)で議論した「序盤の正答速度」との相関（R=0.837）に比べると弱いです。単元別に見ても、相関係数は「中1復習」で0.318、「多項式」で0.326、「連立方程式」で0.368と、いずれも「序盤の正答速度」との相関には及びません。そのため、自信そのものの成績への寄与は相対的に小さく、むしろ「テストの正答率」や「解答速度」などの客観的な計算力指標が高いほど、生徒の主観的な自信も高まりやすい、と考えられます。

(3) 成績層ごとに全く異なるテスト解答戦略
これまでの分析に加え、最後に、テストの成績層別に、テスト中の解答パターンにどのような違いが現れるかを調べました。

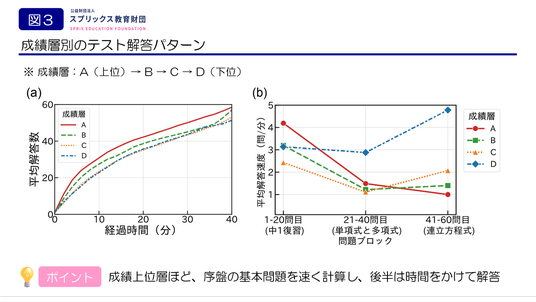
図3. 成績層別のテスト中の解答パターン　全受験者をテストの正答率に基づいて4等分し、成績層を分けました（Aが最上位、以下B、C、Dの順）。左図(a)は各成績層の平均解答数の時間変化、右図(b)はテストの問題ブロックごとの平均解答速度（問/分）を示しています。

ここでは、全受験者をテスト全体の正答率に基づき、成績上位から順にA、B、C、Dの4つの成績層に等分しました。図3(a)は、各成績層が時間経過と共に平均で何問解答したかを示す「進捗曲線」です。成績層Aがテスト開始直後から、最も急なカーブを描き、他の層を引き離し、終始最も速いペースで解答し続けていることが分かります。それ以外の成績層は、より緩やかなカーブを描いており、全体のペースが遅いことが示されています。また、成績層B・Cはテスト終盤に、解答速度を上げている様子が分かります。これは時間が足りず、慌てて選択肢を選んでいることが推測されます。

では、解答ペースの違いは、単元ごとによってどう変化するのでしょうか？それをより詳しく分析したのが図3(b)です。

- 成績層A

序盤の解答速度が最も速く、中盤から終盤にかけては着実にペースを落としています。これは、簡単な問題で時間を確保し、難しい問題に時間をかける効率的なペース配分ができていることを示します。
- 成績層B・C

A層に比べると序盤の解答速度は劣りますが、同様に中盤でペースが落ちます。しかし、終盤になると解答速度が再び上昇する傾向が見られ、特にC層で顕著です。これは終盤に差し掛かり、時間が足りず慌てて問題を解いていることを示唆します。
- 成績層D

この層は序盤から解答速度が比較的高く、終盤にかけてさらに上昇します。これは、テスト開始初期から既に問題に深く取り組むことをやめ、終盤には完全に思考を放棄してランダムに解答している可能性が高いことを示唆しています。

このように、成績上位のグループは序盤で速度を上げ、中盤以降はペースを落として慎重になる「ペース配分戦略」を取る一方で、成績下位のグループほど終盤に解答速度が急上昇する「駆け込み解答」がみられました。

　結果のまとめ

今回のCBT解答ログ分析から、以下の3つの結果がわかりました。

第一に、前学年の復習範囲を含む基礎的な計算問題を「速く、かつ正確に」解ける能力は、テスト全体の正答率と極めて強い相関関係にありました。これは、基礎的な計算能力が、テスト全体の正答率を支える重要な土台であることを示しています。

第二に、生徒の「計算への自信」は、成績が良い原因というよりも、むしろ結果である可能性が示唆されました。「自信があるから成績が良い」のではなく、「計算が速く正確にできる実力があるので、自信もあって成績も良い」と考えられます。

そして最後に、計算テストの正答率の差はテストの解き方にもはっきりと現れました。正答率が高い生徒は、簡単な問題を速く解いて時間を稼ぎ、難しい問題にその時間を使う傾向がありました。一方、正答率が低い生徒は、序盤で時間を使いすぎてしまい、最後は諦めて駆け込みで解答してしまう傾向が見られました。

なお、付録には、本調査から得られた、今後の学習や指導改善のためのヒントも掲載していますので、ぜひご覧ください。本報告は、「基礎学力と学習の意識に関する保護者・子ども国際調査2025」に基づく第四回目の報告です。今後も継続的に調査結果を公表し、国や学年ごとの特徴を明らかにしていく予定です。

調査の詳細は下記よりご確認ください。
調査の詳細（ＰＤＦ）

＜補足＞調査の内容

問題内容：国際基礎学力検定TOFASの計算分野
レベル：中２相当のレベル5
テスト構成：全60問・40分
　・1～20問：中1相当の計算 [例：(5x-9)-(-x-4)]
　・21～40問：単項式・多項式 [例：6ab^2×6a^2b^3]※^2は上付き文字です
　・41～60問：連立方程式 [例：-0.8x+0.3y=0.4 & 0.4x-0.6y=-5.6]
テストの解答形式：選択式（47問）、記述式（13問）
主な指標：開始から5分時点の解答数と正答数、およびテスト全体の正答率(＝正答数÷全60問)
アンケート：計算に対する自信度を５段階で回答

TOFAS（国際基礎学力検定）の詳細は下記よりご確認ください。
TOFAS - 国際基礎学力検定
■公益財団法人スプリックス教育財団　概要
公益財団法人スプリックス教育財団は、社会的支援を必要とする学生に対して奨学金の支給を行うほか、教育に関する調査研究を行いその成果を広く一般に公表し、もって青少年の健全な育成に寄与することを目的としています。

名　　称：公益財団法人スプリックス教育財団
設　　立：2023年4月
代表理事：常石 博之
事業内容：奨学金の支給、調査研究
財団HP ：https://sprix-foundation.org/

企業プレスリリース詳細へ
PR TIMESトップへ

PR TIMES