イタリアの数学者・フィボナッチが紹介したことからその名前をとってつけられた数列「フィボナッチ数列」。造形作家の男性がこの数列を使ったオルゴールを完成させた。「世界のどこにもないもいのを作りたい」と更なる制作への意欲も見せている。
オルゴールにフィボナッチ数列?

歯車を回転させて、リズムを奏でるオルゴール。「フィボナッチ数列」を活用して制作されたオルゴールだ。

静岡県川根本町の造形作家で龍谷大学の客員教授を務める日詰明男さん。
大学で建築を学び、その後、フィボナッチ数列に関連した研究を学生たちに教えながら、27年間の試行錯誤を経て、ようやくオルゴールを完成させた。

造形作家・日詰 明男さん:
数学の研究をしていまして、フィボナッチ数の研究をしているんですけど、あるいは黄金比ですね。それで新しい(複数の異なるリズムを同時に奏でる)ポリリズム音楽ができるんじゃないかと、1995年に思いつきまして、それでまず構想した音楽なんですよ
自然界にもあるフィボナッチ数列
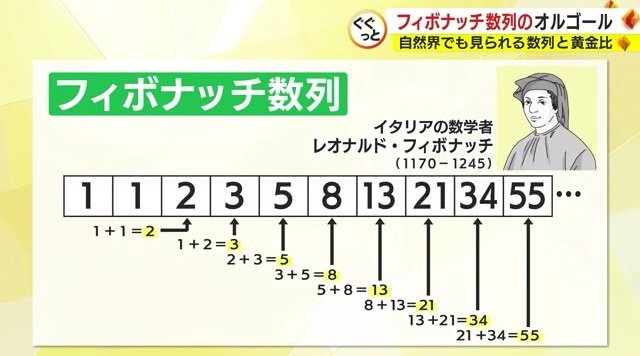
1+1=2、1+2=3、2+3=5、3+5=8…。前の数字2つを足した数字の列「フィボナッチ数列」。イタリアの数学者・フィボナッチが紹介したことからその名がつけられた。

フィボナッチ数列は、身の回りでも見かけることができる。
例えば花がそうだ。ユリの花びらは3枚、ソメイヨシノは5枚、コスモスは8枚、マリーゴールドは13枚、マーガレット21枚というように、この数列の数の花びらをもつ花が多くみられる。
また、木の枝分かれも1本が2本に、2本が3本にと、フィボナッチ数列の数で分かれていくことが多いといわれている。
黄金比とフィボナッチ数列の関係

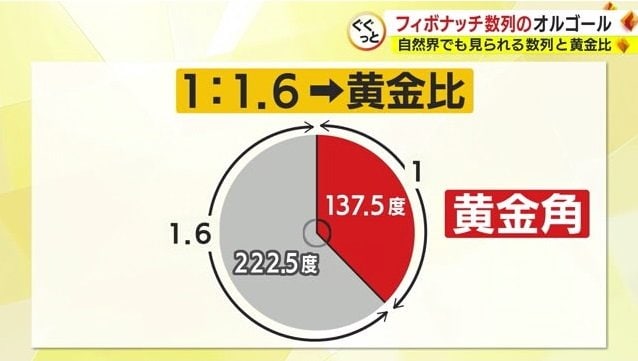
この数列の数字を前の数字で割ると約1.6。数が大きくなるほど、人間が最も美しいと感じる比率「黄金比」に近づいていく。
黄金比は、名刺や免許証、クレジットカードなどに活用されている。

さらに円周をこの黄金比で分けると約137.5度と約222.5度となり、約137.5度は黄金角と呼ばれる。
黄金角は植物の葉がついていく角度にも表れているという。

造形作家・日詰 明男さん:
お茶の葉も例外ではないんです。光をまんべんなく受けることができる、上の葉が下の葉の陰にならない。地震にも強い、倒れにくい、いろんな意味で黄金角は有用で特殊なんですよ。それを数億年前に植物はなぜか発見していて繁栄しているんですね
まだどこにもないものを創り出す

日詰さんはこの数列や黄金比、黄金角に着目。1995年からさまざまな立体作品や音楽を発表してきた。

竹で車輪を表現した作品も、フィボナッチ数列と黄金角を取り入れている。
造形作家・日詰 明男さん:
これは21本の竹でできてるんですけど、その角度が137.5度、黄金角で構成するように組まれています。この時に足音ができますよね、その足音のパターンがオルゴールでお見せした55拍のパターンそのものになっているんです
そして、これまでの作品の集大成と言えるのがオルゴールだ。

造形作家・日詰 明男さん:
最初の歯車の歯数が5です。この歯車で次の歯車は3+5で歯数が8の歯車。次が5+8=13ですから13拍のリズムの歯車ですね。その上が13+8ですから21拍のリズム、その上が34拍、その上が55拍とフィボナッチ数列の拍数(歯数)になっています。フィボナッチ数ですから、その数で無限に増やせるんですよ、歯車が。なおかつ歯車にある法則でボッチが取り付けてあります。規則正しく並んでないんですが法則はあります。この全体のボッチの配置が自己相似といって、入れ子状のパターンになってるんですよ。だから面白い音楽ができる、そういう特徴を持っています
持ち手を1周1秒のペースで回すと、6枚の歯が回し始めの状態に戻るまで約5日間かかるそうだ。
27年かけてオルゴールを完成させた日詰さん。次に制作したい作品は。

造形作家・日詰 明男さん:
新しいものしか作りたくないんですね、普通の家を作るなんて全然何もわくわくしないし、音楽にしてもデザインにしても建物にしても、世界のどこにもないものをこれからも作り続けていきたい
(テレビ静岡)






